- 기본 개념
모평균이 독립적인 셋 이상의 집단 간에 차이가 있는지 검정하는 분석이다.
가정)
1. 각 집단별로 정규분포를 따라야 한다. (정규성)
2. 집단의 분산은 서로 동일해야 한다. (등분산성)
3. 표본의 수가 충분히 커야 한다.
- 집단 간 변동 (Between group variation)
전체 변동 중 모형에 의해 설명되는 변동이다. 아래와 같이 집단 내에서 평균으로부터 퍼져 있는 정도는 비교적 작지만, 세 집단의 평균이 전체 평균으로부터 퍼져 있는 정도는 크다. 따라서, 집단 간의 변동이 크다고 볼 수 있다.

- 집단내 변동 (Within group variation)
전체 변동 중 모형에 의해 설명되지 않는 변동이다. 각 집단이 집단 내에서 각각의 평균으로부터 어느 정도 떨어져 있는지를 나타내는 값이다. 아래와 같이 전체 집단 간의 평균의 차이는 작지만 집단내에서 값들의 퍼진 정도가 큰 것을 확인할 수 있다.
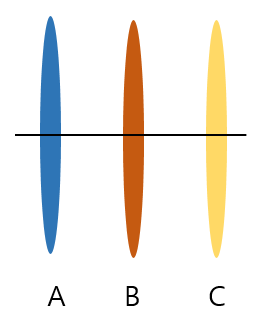
- 총 변동 (Total variation)
총변동은 개별 값들이 전체 평균으로부터 어느 정도 떨어져 있는지를 나타내는 값으로 집단 간 변동 + 집단내 변동 값으로 나타낼 수 있다.
- 집단 간의 변동이 크고, 집단내의 변동이 작을수록 집단 사이의 평균 차이가 존재할 것이다. (그림 1)
- 집단 간의 변동이 작고, 집단내의 변동이 클수록 집단 사이의 평균은 차이가 없을 것이다. (그림 2)
- 검정 과정
H0(귀무가설): 모든 집단의 모평균은 동일하다.
H1(대립 가설): 적어도 한 집단의 모평균은 다른 집단과 다르다. (not H0)
검정 통계량(F) = 집단 간 평균 변동 / 집단내 평균 변동
→ 검정 통계량이 클 때 H0을 기각하고 유의한 결과를 낸다. 그렇기 때문에 집단 간의 평균 변동이 크고, 집단내의 평균 변동이 작을수록 유의하고 적어도 한 집단의 모평균이 다르다는 결과가 나온다.
집단 간 평균 변동 = 집단 간 변동 / (집단 수 - 1)
집단내 평균 변동 = 집단내 변동 / (전체 개체 수 - 집단 수)
- 통계 모형

- ANOVA Table
| 변동 원인 | 자유도 | 제곱합 | 평균제곱 | F 값 | P-Value |
| 집단간(처리) | t - 1 | SSB | MSB = SSB/(t - 1) | F = MSB / MSW | |
| 집단내(오차) | t(n - 1) | SSW | MSW= SSW/t(n-1) | ||
| 전체 | nt - 1 | SST |
- 예시
| ID | A | B | C |
| 1 | 16 | 10 | 12 |
| 2 | 12 | 5 | 8 |
| 3 | 14 | 11 | 6 |
| 4 | 6 | 6 | 2 |
| MEAN | 12 | 8 | 7 |
A, B, C 세 집단이 있다고 가정하고 각각의 관측 값과 각 집단의 평균값을 표에 작성하였다. 세 집단의 평균이 차이가 없다는 것을 귀무가설로 가정하고 이를 검정해보자.
- 모형 계산 식
t (집단 수) = 3, n (각 집단의 관측 값) = 4, 전체 평균 = 9
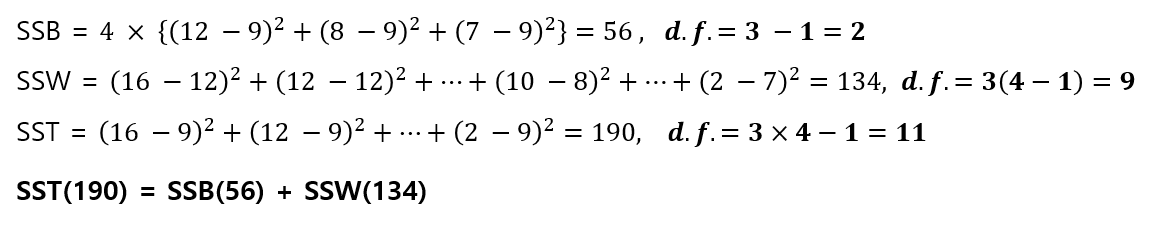
- ANOVA Table
| 변동 원인 | 자유도 | 제곱합 | 평균제곱 | F 값 | P-Value |
| 집단간(처리) | 2 | 56 | 28 | F = 28 / 14.89 = 1.88 |
0.2079 |
| 집단내(오차) | 9 | 134 | 14.89 | ||
| 전체 | 11 | 190 |
# F 분포에서 P-Value를 구하는 코드
1 - pf(1.88, 2, 9) # pf(F 값, d.f.1, d.f.2)
결론적으로, F 값이 1.88으로 작고 p-value가 0.2079로 유의 수준 0.05보다 크기 때문에 귀무가설을 기각할 수 없다.
따라서, 세 집단의 평균에 차이가 없다고 볼 수 있다.
'Statistics' 카테고리의 다른 글
| [Statistics][Regression] 비선형 회귀모형(로지스틱 회귀모형; Logistic Regression) (0) | 2021.10.14 |
|---|---|
| [Statistics][ANOVA] 분산분석(ANOVA) 기본개념/ 독립 이표본 t-검정(Independent two-sample t-test) (0) | 2021.09.09 |
| [Statistics][Time Series Analysis] 2. 시계열 회귀분석 (0) | 2021.07.12 |
| [Statistics][Time Series Analysis] 1. 시계열 분석 기본 개념 (0) | 2021.07.12 |




댓글