[Statistics][ANOVA] 분산분석(ANOVA) 기본개념/ 독립 이표본 t-검정(Independent two-sample t-test)

•  설명변수(X)와 반응 변수(Y)에 따라 통계분석을 하기 위해 사용하는 방법을 다르게 적용한다.

통계분석	설명변수(X)	반응변수(Y)
회귀분석	연속형	연속형
분산분석	이산형	연속형
로지스틱 회귀분석	연속형	이산형
분할표	이산형	이산형

 

• 분산분석의 기본 개념

분산분석(ANOVA)은 세 개 이상 집단들의 평균들 간에 차이가 있는지를 검증하는 통계분석 기법이다. 각 집단들의 표본으로부터 표본 평균값들이 얼마나 차이가 나는지 산출한다. 이때, 표본 평균의 값들이 비슷하다면 모집단의 평균들이 같다고 볼 수 있고, 차이가 난다면 모집단의 평균들에 차이가 있다고 결론을 낸다.

 

예를 들어, 연령대별(20대, 30대, 40대,...) 총소득금액 차이를 알아볼 때 분산분석을 사용할 수 있다. 

 

- 분산분석의 가정

 

1) 집단들은 서로 독립이어야 한다. (독립성)

2) 각 집단들은 정규분포를 따른다.(정규성)

3) 각 집단들은 일정한 분산을 갖는다.(등분산성)

 

• 독립 이표본 t-검정(Independent two-sample t-test)

분산분석을 들어가기 전에 독립적인 두 집단 간에 서로 차이가 있는지 알아보는 독립 이표본 t-검정(Independent two-sample t-test)에 대해서 알아보자. 

 

두 집단의 평균이 동일하다는 가정 하에서 표본 평균들의 차이를 계산한다. 이때, 두 집단의 모평균이 동일하다면 차이 값이 0일 것이다.  

 

- 귀무가설(H0): 증명하려는 가설 / 대립 가설(H1): 새로운 사실, 귀무가설과 반대의 가설

 

다음과 같이 모 분산이 동일하고, 정규분포를 따르는 두 집단 X, Y가 있다고 가정한다. 

 

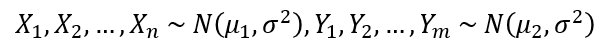
두 집단 X, Y의 평균에 차이가 있는지 알아보기 위해 두 집단의 평균이 같다는 것을 귀무가설로 설정하고 가설을 세운다.

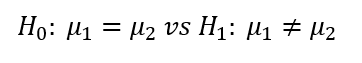
귀무가설을 검증하기 위해 검정 통계량은 t-분포를 따르고, (표본 평균의 차이/ 표본오차)로 계산한다.

 

1) 모 분산이 동일한 경우

두 모집단의 분산이 같을 경우 두 표본을 합하여(pooled) 오른쪽과 같이 모 분산을 추정한다. 그리고 이 추정한 분산 추정량(Sp)을 표준오차를 계산할 때 사용해준다. 

 

2) 모 분산이 동일하지 않은 경우

 

두 모집단의 분산이 다를 경우 각각의 모 분산을 추정하여 표준오차를 계산한다. 

 

→ 두 모집단의 분산이 같은지 다른지 검증하기 위해서는 F-test를 실시하여 판단한다.  F- test는 아래와 같이 분산이 같다는 것을 귀무가설로 설정하고 가설검정을 한다. 

 

가설 검정을 한 결과, 가설을 기각할지 채택할지 판단하기 위해서는 p-value(유의 확률) 값으로 비교한다. p-value는 일반적으로 검정 통계량으로부터 나오는 꼬리 부분 면적이다. 

 

[출처] https://slate.com/technology/2017/08/how-will-changing-the-p-value-threshold-affect-the-reproducibility-crisis.html

 

단측 검정일 경우(가설검정 시 부등호: > or <) 한쪽 면의 p-value 값만을 계산해주면 되기 때문에 그대로 값을 사용하지만, 양측 검정일 경우 (가설검정 시 부등호: =) 양쪽의 p-value를 계산해야 하기 때문에 2를 곱해서 계산한다. 

 

이 p-value를 사용하여 의사결정을 내리는데, p-value가 유의 수준(a-level, 알파 레벨) 보다 크면 기각할 만 근거가 없으므로 귀무가설을 기각할 수 없게 된다. t-test를 예로 들면 두 평균이 같다는 귀무가설을 기각할 수 없으므로 두 집단의 평균이 같다고 생각할 수 있다.

 

반면에, p-value가 유의 수준(a-level, 알파 레벨) 보다 작으면 유의수준하에서 귀무가설을 기각할 만한 근거가 있다고 판단하여 귀무가설을 기각하고 대립 가설을 채택한다. t-test에서 H1을 채택하므로 두 집단의 평균이 다르다고 보는 것과 같다. 

 

[출처] https://www.investopedia.com/terms/p/p-value.asp

 

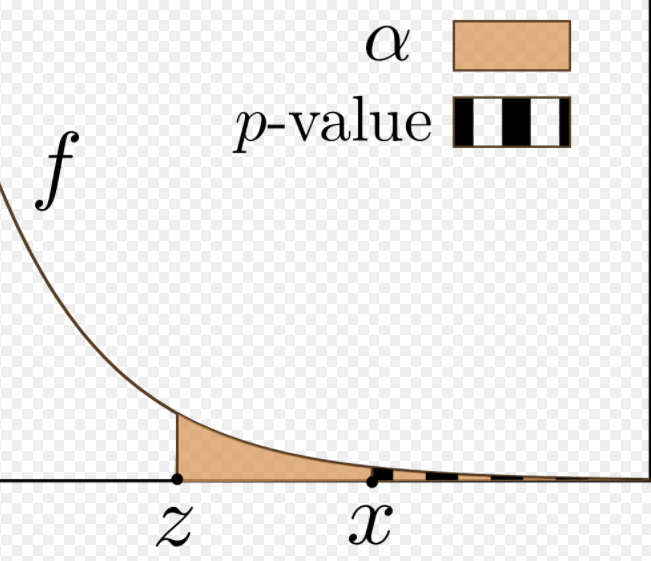
유의 수준은 일반적으로 0.05 정도로 설정하고 판단하는 경우가 많다. 그러나 최근에는 연구에 따라 유의 수준을 설정하는 값이 달라지기도 하고 p-value가 충분히 작은지로 판단하기도 한다. 

 

독립 이표본 t-검정의 절차 

1. 두 집단이 정규분포를 따르는지 파악한다. 
2. 두 집단의 평균과 표준편차 값을 산출한다. 
3. f-test를 이용하여 두 집단의 모 분산이 동일한지 판단한다. 
4. 두 집단의 평균이 같다는 가설을 세우고 t-test를 이용하여 가설을 검정한다.