[Statistics][Time Series Analysis] 2. 시계열 회귀분석

• 시계열 데이터는 일반적인 회귀 분석이 어렵다.

→ 회귀 분석은 기본적으로 서로 독립이라는 가정을 갖는데, 시계열 데이터는 이러한 자기 상관 기본 가정을 위배하기 때문이다.

 

추세를 이용한 회귀 분석

 

시계열 Zt는 추세만을 이용하여 아래와 같이 표현할 수 있다. 

Zt = TRt + Et
Zt : 시점 t에서의 관측값
TRt : 시점 t에서의 추세
Et : 시점 t에서의 오차항

 

함수별 추세선

그림 (1)과 같이 TRt = B0 로 상수항을 가지면 추세가 없는 경우에 해당한다.

그럼 (2), (3)과 같이 TRt = B0 + B1t (B1 >0 or B1 <0) 이면, 일차 선형 추세로, 시계열 자료가 시간에 정비례할 때 해당한다.

그림 (4), (5), (6), (7)은 다항 추세 모형에 해당하는 그래프로 B1, B2 의 부호와 크기에 의해 구분된다.

 

다항 추세 모형은 아래와 같이 확장할 수 있다.

다항 추세모형

→ 선형 모형으로 예측 그래프를 그렸을 때,

   데이터가 독립이 아니기 때문에 상승 추세와 하락 추세의 클러스터링(일정 시기 하락 추세가 지속되고 전환 후 상승 추세가 지속되며 군집이 생기는 현상)이 생길 수 있다.

 

자기 상관 검정

 

시계열 자료는 시간의 흐름에 따라 측정된 자료이다.

따라서, 현재의 값은 과거의 값에 영향을 받게 되기 때문에 자기 상관이 항상 존재한다고 생각해도 무방하다.

 

일반적으로 cor(x, y)와 같이 2개의 변수 사이의 상관관계를 분석하지만, 시계열 데이터에서의 상관 관계는 cor(Xn, Xn-1)로 한 변수에서 시차 사이의 상관 관계를 분석한다.

 

• k차 표본 자기 상관계수

K차 표본 자기상관계수 식

오차항이 1차 자기 상관을 가지는 경우 로우(p) 값이 0인지 아닌지 가설을 세우고, 더빈 - 왓슨 테스트로 검정할 수 있다.

 오차항의 1차 자기상관 식

로우(p)가 0이면 Et와 Et-1간의 상관관계가 없으므로 자기 상관이  없다는 것을 의미하고, 0보다 큰 값이면 양의 상관, 0보다 작은 값이면 음의 상관 관계가 있음을 의미한다.

1차 자기상관 검증식

→ 그러나, 더빈 - 왓슨 테스트는 1차 자기 상관이 있는지 만을 검정하기 때문에 다양한 형태의 자기 상관을 검정하는 것은 불가능하다.

 

계절 효과

1. 고정 계절 변동

     아래와 같이 주기가 일정한 변동으로 가변수와 삼각함수를 이용하여 시계열 회귀 분석을 할 수 있다.

고정 계절 변동

  2. 확산 계절 변동

     

     아래와 같이 주기가 일정하지 않고 점차 확산되는 형태의 주기를 갖는 변동으로 삼각함수를 이용하여 회귀 분석을 할 수 있다.

확산 계절 변동

   3. 가변수

      계절요인을 반영한 가변수 시계열 모형은 다음과 같다.

가변수 시계열 모형

  만약, D가  성별 데이터라고 한다면 D1(여자) =1, 다른 변수 = 0

  D2(남자) = 1, 다른 변수 = 0으로  더미 변수를 생성하여 모형을 세운다.

 

    4. 삼각함수

       1)  고정 계절변동

고정 계절변동 식

       2) 확산 계절변동

 

확산 계절변동 식

       고정 변동과 달리 확산 계절변동에서는 시간 변수인 t(time)을 곱한 교호 작용을 추가해준다.

 

  Airpassenger data 분석

: 추세와 계절성을 가지고 확산 계절 변동을 가지고 있는 데이터 셋

 

선형 추세 모형으로 예측할 시 데이터의 추세를 제대로 따라가지 못한다. (AP ~ time)

선형 추세모형 적합

2차 함수 모형의 다항 추세 모형은 선형 추세 모형보다는 추세를 잘 적합하지만, 계절 주기까지는 따라가지 못한다. (AP ~ time + time^2)

다항 추세모형 적합

고정 계절 변동의 삼각함수를 이용하여 회귀 모형을 적합시킨 결과 추세의 방향과 계절의 주기는 따라가지만, 계절 변동의 폭이 일정하기 때문에  Airpassenger Data의 계절 주기가 확산되고 있는 부분은 고려하지 못한다. (AP~time+time2+sin1+sin2+sin4+sin8+cos1+cos2+cos4+cos8)

고정계절변동 삼각함수 추세모형 적합

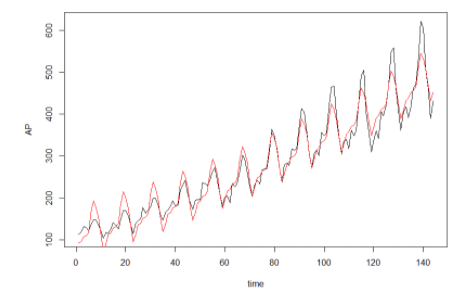
확산 계절 변동의 삼각함수를 이용하여 회귀 모형을 적합시킨 그래프로 Airpassenger Data의 시계열 변동을 가장 잘 적합시킨다.

추세와 계절 주기도 대부분 일치하고, 점차 확산되는 계절 변동 폭도 잘 나타내 주고 있다.

(AP~time+sin1+sin2+cos1+cos2+time*sin1+time*sin2+time*cos1+time*cos2)

확산계절변동 삼각함수 추세모형 적합

 

[출처: 박유성, 김기환, SAS/ETS를 이용한 시계열 자료분석 1, 자유아카데미(2002)]