[Deep Learning][Deep Learning from Scratch] 신경망
사이토 고키, 「밑바닥부터 시작하는 딥러닝」, 개앞맵시, 한빛미디어, Chapter 3의 내용을 정리하고 공부한 페이지입니다.
- 신경망

신경망은 가중치 매개변수의 적절한 값을 데이터로부터 자동으로 학습할 수 있는 능력을 가진다. 위의 모형과 같이 기본적으로 입력층(0층), 은닉층(1층), 출력층(2층)의 구조로 구성된다.
- 활성화 함수
활성화 함수는 입력 신호의 총합이 활성화를 일으키는지를 정하는 역할을 한다.

편향을 1이라고 했을 때, 오른쪽의 그림(활성 함수 처리 과정)을 보면 가중치와 입력 신호를 조합하여 a라는 결과가 된다. 이를 활성화 함수 h( )에 통과시켜 y라는 노드로 변환되는 과정이다.
- 계단 함수 (Step Function)
일반적으로 활성화 함수는 임계 값을 넘으면 1을 변환하고 넘지 않으면 0으로 변환되기 때문에 계단 함수의 형태를 띤다. 0을 경계로 0 보다 작은 값들에서는 0 값이, 0 보다 큰 값들에서는 1 값이 결과로 출력된다.

이후 내용은, 이러한 일반적인 경우가 아닌 활성화 함수를 다른 함수로 변경하는 것에 대해서 살펴볼 것이다.
- 시그모이드 함수 (Sigmoid Function)
신경망에서 자주 이용하는 활성함수로 0 과 1 사이에서 값을 가진다. 아래와 같은 함수 식을 가지며, e가 자연상수(2.7182..)이므로 x에 값을 넣으면 값으로 출력된다. 예를 들어, x = -1일 때, y = 0.7311 값을 가지고 x = 2일 때, y = 0.1192 값을 가진다.

시그모이드 함수의 그래프를 그리면 아래와 같이 S자 모형의 곡선으로 그려진다.
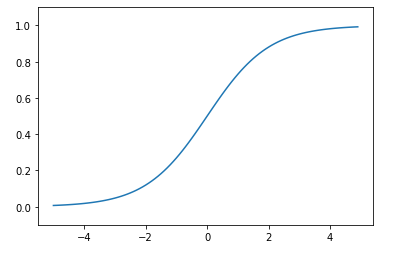
→ 계단 함수와 시그모이드 함수의 가장 큰 차이점은 계단 함수가 0과 1 중 하나의 값만 가지는 반면 시그모이드 함수는 실수 값을 가진다. 퍼셉트론에서는 뉴런 사이에 0과 1이 흘렀지만, 신경망 학습에서는 연속적인 실수가 흐르는 것이다.
두 함수의 공통점은 입력에 상관 없이 0과 1 사이에서 출력 값을 가진다. 또한, 두 함수 모두 비선형 함수이다. 신경망에서는 선형 함수를 사용할 수 없고, 비선형 함수를 사용해야 한다.
만약, 선형 함수를 이용하면 직선의 형태이기 때문에 층을 깊게 하는 것의 의미가 없어진다. C나 C를 세 번 곱한 값이나 상수 값으로, 함수의 모양은 같기 때문이다.

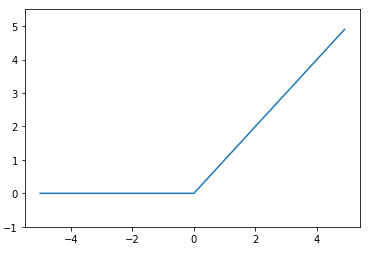
- ReLU 함수 (Rectified Linear Unit)
ReLU 함수는 입력이 0을 넘으면 그 입력을 그대로 출력하고, 0 이하이면 0을 출력하는 함수이다. 신경망 분야에서 시그모이드 함수를 많이 썼지만, 최근에는 ReLU 함수도 많이 사용하는 추세이다.